How to measure black hole mass?
Measuring of black hole masses is a relatively straightforward thing to do and, apart from measuring spin, one does not need any super-sophisticated equipment. An ordinary telescope is enough to do the job, but of course the further distant the target object is the larger telescope is necessary.
The technique that is used is a pretty old one and simply involves Kepler's laws. However, not every black hole can be measured like that. The method best applies to stellar black holes that are part of a binary system and live together with a companion star. A vast majority of stars in the Galaxy are in fact part of a binary or higher-order system, solitary stars like our Sun make only about 20%. Most stellar black holes are therefor expected to have a companion, not mentioning the fact that finding a lonely black hole is merely impossible because there is practically no way to see it if it has nothing to reveal its presence in its vicinity.
To discover a system with a black hole, several things have to be right. Most importantly, the black hole must have an accretion disk around itself. If it had none, it would not produce any radiation and we would only see the companion star. Still it would be possible to guess that there is an unseen component there, but without a disk around it, we are not able to say anything more about it. Accretion disks are hot. The temperature reaches millions of degrees in their inner parts and because of that the photons that are emitted from there have high energies and we see them as X-rays. Outer parts of the disk are cooler and radiate in UV and optical bands. If an object is found that is bright both in optical and in X-rays, it makes for a very good candidate to be a binary system with a black hole.
Once we discover a system where we suspect a black hole orbits a normal companion star, we may study light that comes from the source. The black hole and the star are usually in quite a close distance to each other and no telescope on Earth can resolve the individual components. The light we receive is a mix from both the star and the black hole accretion disk. If the light is dispersed to it's spectrum we find plenty of spectral lines. Some belong to the star, some to the accretion disk. But because the star and the black hole with the disk orbit around each other, each day we observe the the components at a different positions and with a different radial projection of their orbital velocities. This makes the key to measuring the mass.
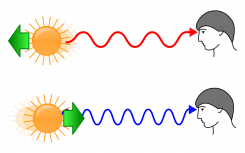
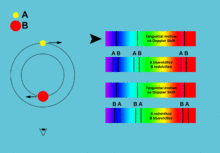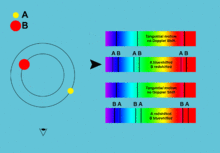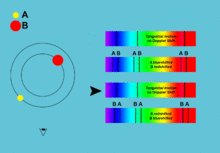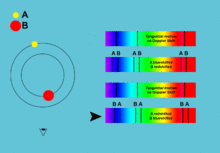
In one part of its orbit the star seems to be moving toward us with positive radial velocity, the other part it seems to recede from us with negative radial velocity. The same with the accretion disk only with an opposite phase. This periodic change in radial velocity can be seen in the spectrum as a tiny shift of spectral lines due to the Doppler effect. The more the lines shift, the faster the object moves. And because the star and the disk move with the opposite phase, their spectral lines move different directions in the spectrum. This allows us to identify which lines belong to which component and to measure the radial velocities for both of them separately.
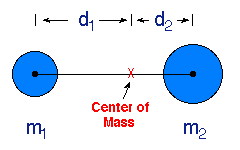
Now it is time to use the Kepler's laws. The first one says that the star and the black hole move along elliptic orbits around a common point, which is where the center of mass of the whole system is. The third one says that the ratio of the third power of the semi-major axis of the elliptic orbit to the second power of the orbital time is constant. The constant is the sum of the two masses times some numerical factor. We do measure the orbital time and thus we can express the average separation of the two components as a function of (yet) unknown masses. Then we know where is the center of mass. At each point, the ratio of the distances from the center of mass to each of the components is the same as the ratio of their masses. We need to know one extra bit of information and that is the orientation of the orbits in space, or simply the orbital inclination, which can be inferred from the temporal variations in the light curves. Putting all the pieces together we have enough information to calculate the individual masses of both parts of the system, the star and the black hole.
